R et python s'imposent aujourd'hui comme les langages de référence pour la data science. Dans cet article, je vais vous exposer la méthodologie pour appliquer un modèle de régression linéaire multiple avec R et python. Il ne s'agit pas ici de développer le modèle linéaire mais d'illustrer son application avec R et python.
Préalable

Pour utiliser R, il faut tout d'abord l'installer, vous trouverez toutes les informations pour l'installation sur le site du projet R :
https://www.r-project.org/
Je vous conseille d'utiliser RStudio pour coder en R, ceci vous simplifiera largement la vie. Dans cet article, je ne présenterai que le code nécessaire donc vous pouvez reproduire le code dans R ou dans RStudio.
https://www.rstudio.com/

Pour utiliser python, il faut l'installer et faire un certain nombre de choix. Le premier étant la version. Dans le cadre de cet exemple, j'utiliserai python 3.6 (l'ensemble des bibliothèques et outils peuvent être utilisés aussi avec python 3.6). Pour une application en data science, il est souvent plus efficace de télécharger Anaconda qui en plus de python propose des interfaces améliorées et toutes les bibliothèques nécessaires en data science. Voici leur site :
https://www.anaconda.com/download/
Pour vous entraîner et travailler de manière collaborative, je vous conseille d'utiliser les Jupyter Notebooks. Si vous préférez un environnement plus classique, Spyder est une bonne solution qui se rapproche de RStudio.
La régression linéaire
La régression linéaire multiple est une méthode ancienne de statistique mais qui trouve encore de nombreuses applications aujourd'hui. Que ce soit pour la compréhension des relations entre des variables ou pour la prédiction, cette méthode est en général une étape quasi obligatoire dans toute méthodologie data science.
Le principe de la régression linéaire : il consiste à étudier les liens entre une variable dépendante et des variables indépendantes. La régression permet de juger de la qualité d'explication de la variable dépendante par les variables indépendantes.
Le modèle statistique sous-jacent est très simple, il s'agit d'une modèle linéaire qui est généralement écrit :
y=constante + beta1 x1 + beta2 x2 + ... + erreur
L'estimation des paramètres de ce modèle se fait par l'estimateur des moindres carrés et la qualité d'explication est généralement évalué par le R².
La qualité de prédiction est généralement mesurée avec le RMSE (racine de la somme des carrés des erreurs).
Les données et le modèle
Dans le cadre de cet exemple, on va utiliser des données simples reliant un nombre de ventes et l'investissement dans différents médias. Le modèle de régression multiple a une variable dépendante y mesurant le nombre de ventes et 3 variables indépendantes mesurant les investissements en terme de publicité par média.
Le chargement des données et des bibliothèques

S'agissant de données au format csv, il est simple de les importer dans R.
Nous utilisont la fonction read_csv2 de R.
Voici le code pour importer les données :
ventes = read.csv("Advertising.csv")
summary(ventes)
Python n'a pas nativement de fonction pour importer des données au format csv. Nous allons donc utiliser la bibliothèque pandas afin d'importer les données. Cette bibliothèque est comprise dans Anaconda. Nous utiliserons aussi numpy et matplotlib pour les visualisations.
Voici donc le code pour importer les données :
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#importer les données Advertising.csv
donnees = pd.read_csv('Advertising.csv', index_col=0)
donnees.head()L'application du modèle de régression linéaire

Nous créons un objet reg_ventes issu du modèle linéaire lm() (la régression linéaire est un cas particulier du modèle linéaire général).
Ce type de modèle est déclaré en utilisant le nom des variables dans les données.
On aura comme modèle : y ~ x1 + x2 +...
Le modèle peut bien sûr être plus évolué (interaction, transformations). Le code est donc très simple.
reg_ventes=lm(Sales~ TV+Radio+Newspaper,data=ventes)
Nous créons maintenant un objet modeleReg qui est le conteneur de notre modèle de régression multiple.
Une fois l'objet créé en utilisant la bibliothèque scikit-learn, nous ajustons le modèle (fit) en utilisant nos données. J'ai donc pris comme variable dépendante y, la variable Sales et comme variables indépendantes toutes les autres variables.
from sklearn.linear_model import LinearRegression
#créer un objet reg lin
modeleReg=LinearRegression()
#créer y et X
list_var=donnees.columns.drop("Sales")
y=donnees.Sales
X=donnees[list_var]
modeleReg.fit(X,y)L'affichage des résultats

Une fois le modèle de régression linéaire ajusté, R propose des sorties proches de celles de nombreux logiciels de statistique.
Summary() affiche les coefficients les significativité et le R². Le RMSE doit par contre être recalculé "manuellement".
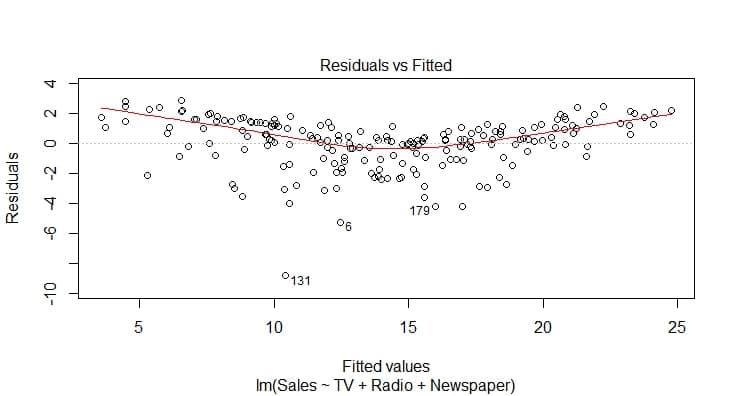
La fonction plot() affiche 4 graphiques aidant à la validation des hypothèses.
#affichage des résultats dont le R²
summary(reg_ventes)
#calcul du RMSE
predictions = predict(reg_ventes, sales)
rmse = mean((sales$sales - predictions)^2)
print(rmse)
#affichage des graphiques
plot(reg_ventes)
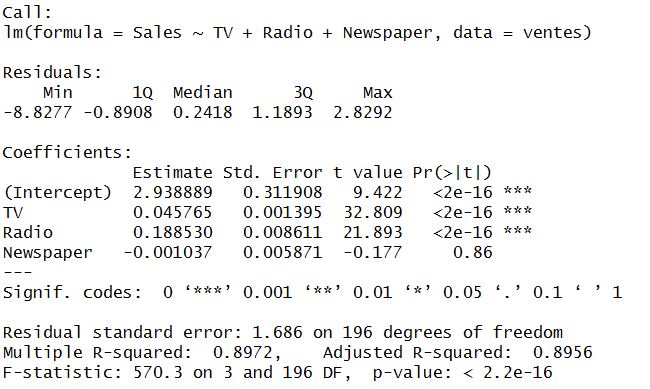

Une fois le modèle ajusté, nous affichons, la constante, les coefficients, le R² et le RMSE.
Nous obtenons deux graphiques (qu'il faudrait mieux préparer) représentant : les valeurs de y en fonction des valeurs prédites avec le modèle de régresssion linéaire et les valeurs de Y en fonction des résidus.
De nombreuses autres analyses sont possibles, mais on a ainsi déjà quelques informations sur notre modèle.
print(modeleReg.intercept_)
print(modeleReg.coef_)
#calcul du R²
modeleReg.score(X,y)
RMSE=np.sqrt(((y-modeleReg.predict(X))**2).sum()/len(y))
plt.plot(y, modeleReg.predict(X),'.')
plt.show()
plt.plot(y, y-modeleReg.predict(X),'.')
plt.show()
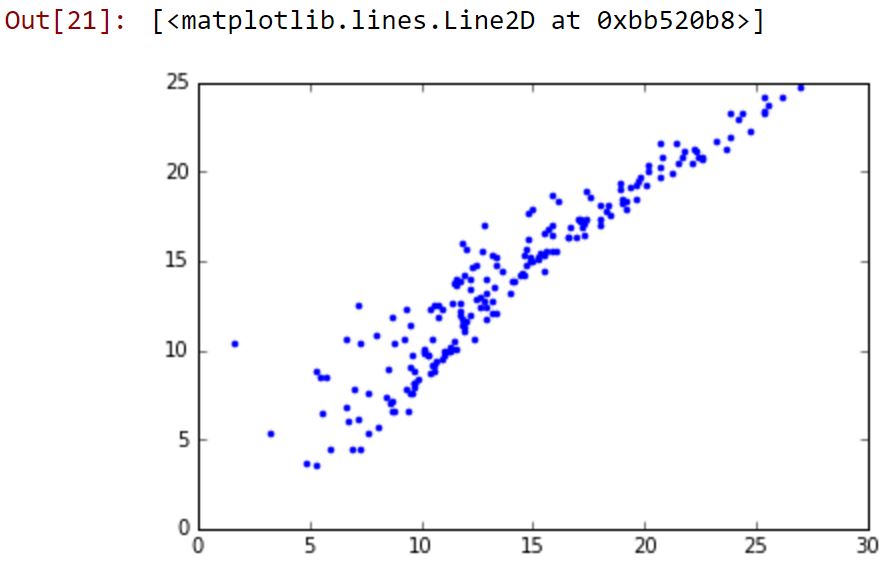
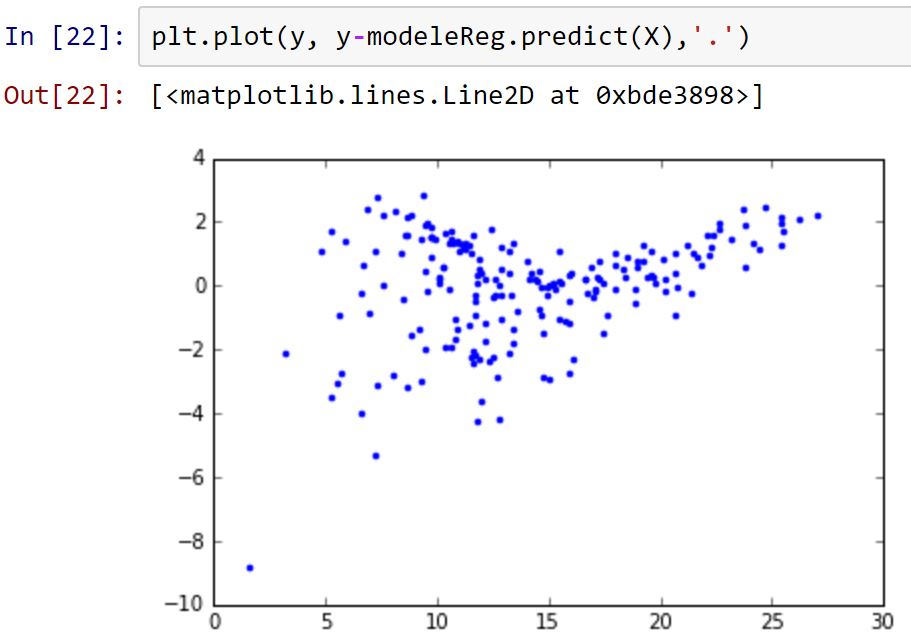
Cette analyse est uniquement illustrative pour vous montrer à quel point ces deux langages sont simples pour ce type de traitement. Ce qui ressort aussi c'est un aspect plus orienté statistique pour R et un aspect plus orienté programmation pour python (du moins en terme de sorties).
Aujourd'hui, la question n'est plus de choisir entre R ou python, ces deux langages ont leurs avantages et leurs défauts. Votre choix doit se faire en fonction des projets que vous rencontrerez dans votre vie de data geek (on peut remplacer geek par scientist, analyst, miner, ....). Mon article sur les langages de la data science vous éclairera aussi à ce sujet.
Le seul conseil à vous donner : essayez-les, entraînez-vous et vous les adopterez très vite.
DÉCOUVREZ NOS FORMATIONS PYTHON ET R !
Partager cet article



Comments 9
Bonjour.
J’aimerai revenir rapidement sur une des phrases de l’article
« Dans le cadre de cet exemple, j’utiliserai python 2.7. Dans le cadre d’une application en data science, il est souvent plus efficace de télécharger Anaconda qui en plus de python propose des interfaces améliorées et toutes les bibliothèques nécessaires en data science. »
Ce n’est plus vrai aujourd’hui. Anaconda propose une version 3.5 (c’est même celle proposé en premier sur leur page de téléchargement), et la quasi-totalité des packages usuels en calcul scientifique/data-science sont portés (voir http://py3readiness.org/).
Une règle applicable est :
projet écrit en python 2.X -> continuer avec, nouveau projet -> python 3.X
Author
Bonjour,
Merci pour cette remarque. La phrase est peut-être un peu mal tournée. Le choix de python 2.7 n’est pas du tout lié au choix d’utiliser Anaconda. Il est vrai qu’Anaconda et la plupart des bibliothèques de data science sont compatibles avec 2.7 et 3.5.
La décision d’utiliser 2.7 ici est purement pédagogique car, (malheureusement), la plupart des ressources sur le web sont encore codées en 2.7. Il est évident que pour un nouveau projet, il est préférable d’utiliser la 3.5 et vivement que 3.5 soit la norme partout !
Emmanuel
Salut,
Est-ce que vous pouvez résoudre cet erreur chez mon code ? J’ai copié votre code e testé avec le dataset différent, mais il prit un erreur.
Voici mon code :
https://gist.github.com/anonymous/2c6e8cfb1393b587281d0a372af7293c
Et les erreurs :
ValueErrorTraceback (most recent call last)
in ()
86 X = donnees[list_var]
87
—> 88 modeleReg.fit(X, y)
89
90 print modeleReg.intercept_
/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/sklearn/linear_model/base.pyc in fit(self, X, y, sample_weight)
510 n_jobs_ = self.n_jobs
511 X, y = check_X_y(X, y, accept_sparse=[‘csr’, ‘csc’, ‘coo’],
–> 512 y_numeric=True, multi_output=True)
513
514 if sample_weight is not None and np.atleast_1d(sample_weight).ndim > 1:
/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/sklearn/utils/validation.pyc in check_X_y(X, y, accept_sparse, dtype, order, copy, force_all_finite, ensure_2d, allow_nd, multi_output, ensure_min_samples, ensure_min_features, y_numeric, warn_on_dtype, estimator)
519 X = check_array(X, accept_sparse, dtype, order, copy, force_all_finite,
520 ensure_2d, allow_nd, ensure_min_samples,
–> 521 ensure_min_features, warn_on_dtype, estimator)
522 if multi_output:
523 y = check_array(y, ‘csr’, force_all_finite=True, ensure_2d=False,
/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/sklearn/utils/validation.pyc in check_array(array, accept_sparse, dtype, order, copy, force_all_finite, ensure_2d, allow_nd, ensure_min_samples, ensure_min_features, warn_on_dtype, estimator)
405 % (array.ndim, estimator_name))
406 if force_all_finite:
–> 407 _assert_all_finite(array)
408
409 shape_repr = _shape_repr(array.shape)
/Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/sklearn/utils/validation.pyc in _assert_all_finite(X)
56 and not np.isfinite(X).all()):
57 raise ValueError(« Input contains NaN, infinity »
—> 58 » or a value too large for %r. » % X.dtype)
59
60
ValueError: Input contains NaN, infinity or a value too large for dtype(‘float64’).
Bonjour Gustavo,
Le problème vient du fait que vous avez des données manquantes dans votre jeu de données et le modèle de régression linéaire de scikit-learn ne gère pas cela.
Il faut donc traiter ces données en amont soit en utilisant .dropna() de pandas soit Imputer() de scikit-learn.
Bonne fin de journée,
Emmanuel
Bonjour,j’ai eu le même problème et je ne veux pas non plus supprimer les données manquants de mon dataframe afin de garder le maximum des informations.
N’y a t il pas une autre méthode de calculer la pente avec des données manquants?
Bonjour,
Vous pouvez imputer les données manquantes en utilisant soit la méthode .fillna() de pandas, soit la classe SimpleImputer() de scikit-learn.
Bonjour ,
s’il vous plait je recherche desesperemment une personne qui s’y connaît en r studio et plus précisément sur l’interpretation des sorties R en regression lineaire , a l’aide !!! , ma licence en depend !
Bonjour,
Et quelles sont les questions que vous vous posez ?
Cordialement,
Emmanuel
Bonjour cher(s) éducateur(s).
j’aime votre page sur les analyses avec R, je veux avoir autant de formation et arriver a conduire mes analyses et interprétation des résultats.
MERCI