Vous avez forcément entendu parler du box-plot que l'on appelle aussi boîte à moustache pour sa forme originale. Ce graphique tout simple permet de résumer une variable de manière simple et visuel, d'identifier les valeurs extrêmes et de comprendre la répartition des observations. Nous vous proposons quelques détails sur ce graphique afin de l'utiliser simplement.
Comment est construit un box-plot
Un box-plot est un graphique simple composé d'un rectangle duquel deux droites sortent afin de représenter certains éléments des données.
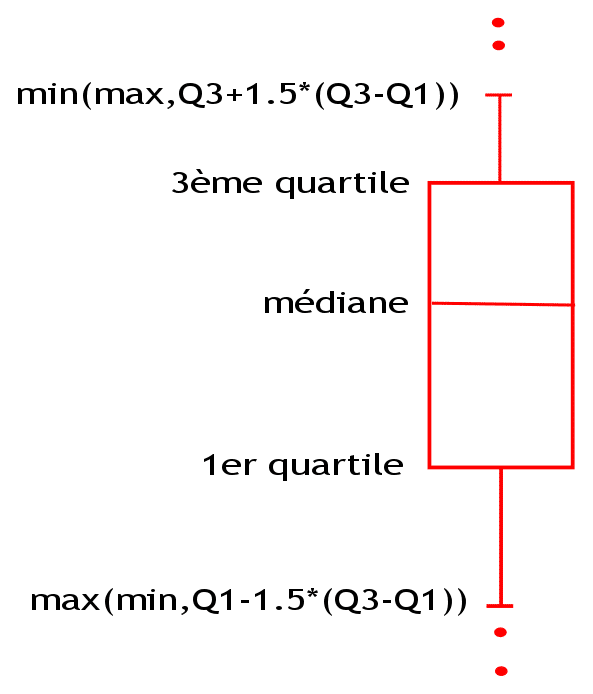
- La valeur centrale du graphique est la médiane (il existe autant de valeur supérieures qu'inférieures à cette valeur dans l'échantillon).
- Les bords du rectangle sont les quartiles (Pour le bord inférieur, un quart des observations ont des valeurs plus petites et trois quart ont des valeurs plus grandes, le bord supérieur suit le même raisonnement).
- Les extrémités des moustaches sont calculées en utilisant 1.5 fois l'espace interquartile (la distance entre le 1er et le 3ème quartile).
On peut remarquer que 50% des observations se trouvent à l'intérieur de la boîte.
Les valeurs à l'extérieur des moustaches sont représentées par des points. On ne peut pas dire que si une observation est à l'extérieur des moustaches alors elles est une valeur aberrante. Par contre, cela indique qu'il faut étudier plus en détail cette observation.
Ce que l'on peut représenter en plus dans un box-plot
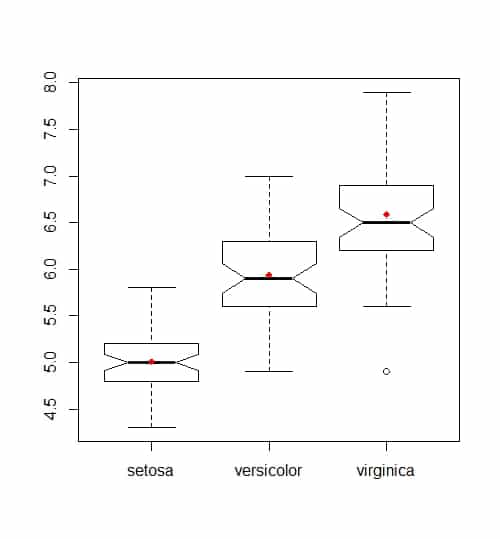
On voit souvent apparaître des box-plot avec des formes différentes ou des signes supplémentaires, en voici quelques uns :
- La croix rouge dans la boîte : lorsqu'une croix rouge apparaît dans le box-plot, il s'agit toujours d'une représentation de la moyenne sur l'échantillon étudié.
- Des boîtes ayant des largeurs variables : il arrive souvent que les boîtes n'aient pas la même taille (en largeur), il ne s'agit pas d'une simple transformation esthétique, la largeur est alors proportionnelle à la taille de l'échantillon. Ceci est spécialement intéressant dans le cas de comparaison de groupes d'observations pour lesquelles la taille des groupes n'est pas homogène.
- Des boîtes avec une boîte qui se ressert autour de la médiane (notched) : Cette représentation permet de visualiser un intervalle de confiance à 95% autour de la médiane. Les points où la boîte se ressert représentent les bornes de cet intervalle.
On le calcule avec la formule suivante :
médiane +/- 1.57 * (Q3-Q1)/racine(N) avec Q1 1er quartile, Q3 3ème quartile et N taille de l'échantillon.
Comme on peut le voir dans le box plot représenté avec R, toutes ces options peuvent être ajoutées simultanément au box-plot.
Quand utiliser un box-plot
Il est intéressant d'utiliser les box-plot lorsqu'on désire visualiser des conepts tels que la symétrie, la dispersion ou la centralité de la distribution des valeurs associées à une variable.
Ils sont aussi très intéressant pour comparer des variables basées sur des échelles similaires et pour comparer les valeurs des observations de groupes d'individus sur la même variable.
Les box-plot dans R
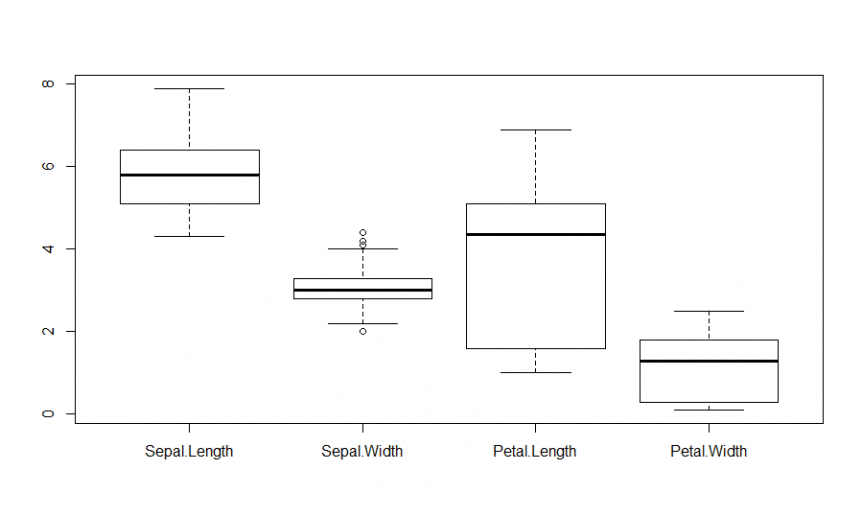
R vous permet de dessiner des box-plots de manière simple et rapide grâce à la fonction boxplot. Ainsi si on prend les données iris se trouvant dans R, on dessine un box-plot standard en utilisant les 4 variables quantitatives du jeu de données :
data(iris)
boxplot(iris[1:4])Si on désire utiliser une variable qualitative comme variable de groupe, on peut utiliser le code suivant :
boxplot(iris$Sepal.Length~iris$Species)On utilise donc une formule permettant de représenter les box-plots associés à chaque espèce d'iris pour la longueur des sépales.
Pour représenter un box-plot notched et dont la taille dépend de la taille de chaque échantillon, il suffit d'utiliser le code suivant :
boxplot(iris$Sepal.Length~iris$Species,varwidth = TRUE, notch = TRUE, outline = TRUE)De nombreuses autres options sont disponibles, vous les trouverez dans cette description de la fonction boxplot.
Les autres logiciels pour les box-plots
Tous les logiciels de statistique et d'analyse de données permettent de dessiner des box-plots.
Les liens intéressants
Des descriptions des boîtes à moustaches peuvent être trouvées sur beaucoup de sites web. En voici quelques unes :
Les références
S'il fallait n'en citer qu'une, ça serait :
John W. Tukey (1977). Exploratory Data Analysis. Addison-Wesley.
Pour la version notched, on peut voir :
John M. Chambers (1983). Graphical methods for data analysis. Wadsworth International Group.
Découvrez nos formations en analyse de données et en statistique
Découvrez nos formations R
Partager cet article


Comments 13
Pingback: Quelles statistiques utiliser pour décrire une variable ? - STAT4DECISION
J’ai apprécié cet article et je désir m’abonner à votre newsletter our obtenir plis de contelus
un article interressant!!
Bonjour, je voudrai avoir un ou des scripts qui vont me permettre de représenter dans un boxplot la médiane et la moyenne
Bonjour,
Dans le box plot, la croix rouge représente la moyenne et la barre centrale de la boîte représente la médiane quelle que soit l’outil utilisé.
Si les extrémités des moustaches sont calculées en utilisant 1.5 fois l’espace interquartile (la distance entre le 1er et le 3ème quartile), pour quelle raison les longueurs de ces segments ne sont-ils pas identique de part et d’autre de la boîte ?
Bonjour,
Si le minimum ou le maximum est atteint alors la moustache s’arrête, d’où l’aspect non symétrique.
est ce qu’il peut arriver qu’on ait des valeurs négatives pour le minimum Q1-1,5(Q3-Q1)
Bonjour Diane,
La valeur associée à la borne inférieure dépend de vos données. Si vous avez des données négatives, il arrivera souvent que cette borne soit négative.
Cordialement,
Emmanuel
Quelle est l’intérêt de l’extrémité des moustaches ? Comment utilise-t-on cette valeur de 1.5 fois l’espace interquartile ?
Et, est-ce que c’est toujours cela que ça représente ou parfois, ces extrémités représentent d’autres valeurs ?
Bonjour,
L’intérêt est de repérer les données qui sont au-delà de cet intervalle. On aura souvent tendance à les identifier comme des valeurs extrêmes.
La distance entre le boîte et l’extrémité représente soit 1.5 fois l’espace interquartile soit la distance au maximum (ou minimum pour la moustache inférieure).
Bien cordialement,
Emmanuel
très intéressant
Je suis chercheur suis satisfait de la réponse à ma question ,ces recherches m’aideront aux analyses des donneés