Vous avez déjà entendu parler de la régression PLS, des moindres carrés partiels, de la régression Partial Least Square. Ces termes désignent une méthode statistique qui a vu le jour au début des années 1980 et qui connaît aujourd’hui de nombreuses applications dans des domaines extrêmement variés.
Il ne s’agit pas ici de faire un cours sur la régression PLS mais de mettre en avant ses forces et faiblesses tout en évoquant les moyens de la mettre en oeuvre.
Si vous désirez aller plus loin, je vous conseille le très bon ouvrage de Michel Tenenhaus sur le sujet que vous trouverez ici. Si cet ouvrage vous paraît trop technique ou si vous préférez être former par des experts, venez suivre l’une des formations de STAT4DECISION pour comprendre comment utiliser cette méthode.
Le principe de la régression PLS
Comme son nom l’indique, la régression PLS est une méthode de régression avec laquelle on va tenter d’expliquer des variables Y par des variables X.
On utilise un algorithme itératif assez simple basé sur des composantes (pour ceux qui sont familiers avec l’analyse en composantes principales, il s’agit de composantes du même type) et des régressions linéaires entre ces composantes.
L’algorithme de la régression PLS est né des recherches de Svante Wold au début des années 1980 qui lui-même s’est inspiré des travaux de son père Herman Wold.
Avec le développement des algorithmes NILES et NIPALS, Herman Wold a mis en place les bases de la régression PLS. Par la suite, il s’est ensuite orienté vers l’approche PLS (aussi nommée PLS Path Modeling, à ne pas confondre avec la régression) et son fils a fait évoluer ces algorithmes pour aboutir aux algorithmes PLS1 et PLS2.
Ses forces
La prise en compte de la multicolinéarité
Le principal avantage de la régression PLS et ce qui lui donne une forte supériorité face à la régression linéaire multiple (dite OLS) est la possibilité d’avoir des variables explicatives fortement corrélées (ce qu’on appelle la multicolinéarité). Ceci s’explique par le fait qu’on utilise des composantes orthogonales les unes aux autres issues des variables explicatives.
La gestion de tableaux écrasés
Lorsque le nombre d’observations est faible et le nombre de variables est élevé, la régression ordinaire ne peut plus être appliquée. La régression PLS permet de traiter ce type de données du fait de la réduction de dimension induite par l’utilisation de composantes.
La possibilité d'avoir plus d'une variable dépendante
Avec l’introduction de l’algorithme PLS2, on peut expliquer un groupe de variables Y par un groupe de variables X. On utilise pour cela des composantes PLS au niveau des Y. On se rapproche ainsi des méthodes dites de tableaux multiples.
Le traitement des données manquantes
La régression PLS offre une méthodologie originale pour le traitement des données manquantes. En effet, la régression PLS est basée sur un algorithme itératif pouvant travailler sur des données incomplètes. On utilisera donc les données disponibles pour construire les composantes et il n’y aura pas besoin de compléter les données manquantes.
Ses faiblesses
Le choix du nombre de composantes
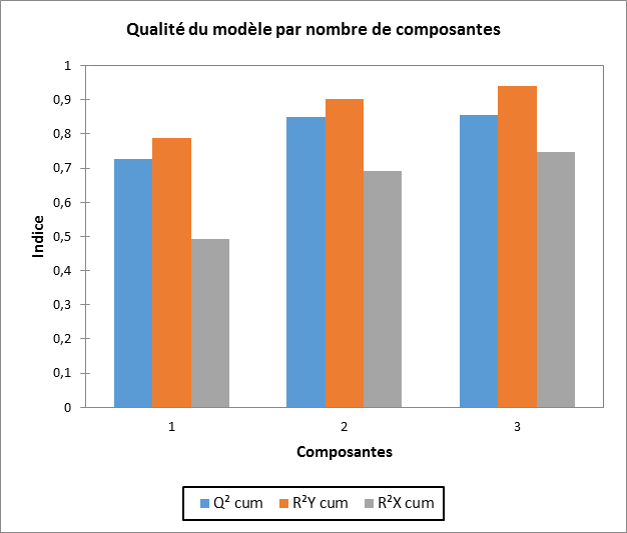
C’est un problème récurrent dans beaucoup de méthodes d’analyse de données. De nombreuses méthodes existent mais elles doivent toujours être validées par la connaissance des données et la cohérence du modèle. On utilise généralement des techniques basés sur la validation croisée et l’indice Q2. Les méthodes proposées dépendront des logiciels utilisés.
La complexité des sorties
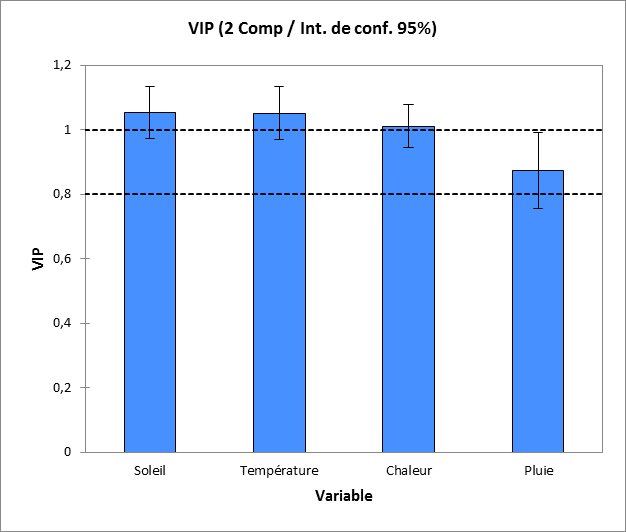
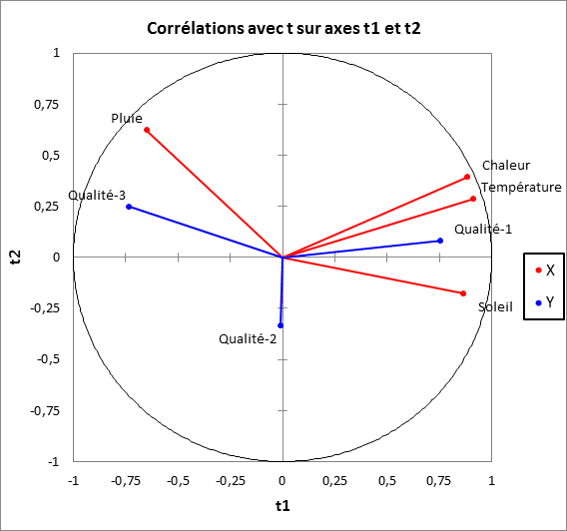
Une régression PLS est une combinaison de transformations répétées de manière itérative. Il s’agit donc de transformer les variables en composantes et de relier les composantes. Les sorties d’une régression PLS concernent toutes les étapes de ce processus et offrent une grande richesse d’interprétation à condition de maîtriser les différents types de sorties (les composantes des X, celles des Y, les coefficients du modèle, les VIP…).
La linéarité du modèle
Même si la régression PLS est basée sur un modèle plus évolué que la régression linéaire ordinaire, le modèle sous-jacent reste un modèle linéaire (les composantes sont des combinaisons linéaires des variables et les relations entre les composantes de X et de Y sont aussi linéaires). Des évolutions non linéaires existent mais elles restent confidentielles et les méthodes de régressions non linéaires sont toujours plus efficaces pour traiter la non linéarité.
Quand utiliser la régression PLS ?
La régression PLS doit être utilisée lorsque la régression linéaire multiple ne peut pas s’appliquer. En particulier en cas de forte multicolinéarité ou lorsqu’on a plus de variables que d’individus. C’est pour cette raison qu’elle trouve des applications en chimiométrie, en analyse de données médicales ou en traitement des données de type OMICS. Elle peut aussi être appliquée dans des domaines plus classiques de l’analyse de données dès qu’on a des variables explicatives fortement corrélées. Il faut bien noter qu’elle ne recherche pas de relations non linéaires et qu’elle ne sera donc pas adaptée à ce cas.
Quel logiciel utiliser pour la régression PLS ?
La plupart des logiciels de statistiques et d’analyse de données possèdent une version simple de la régression PLS. On aura tendance à préférer R pour ce type d’analyses avec la possibilité de faire des régression PLS 1 et 2 (dans le package PLSdepot).
Si vous désirez aller plus loin, trois logiciels se détachent des précédents :
- Simca-P : c’est le logiciel développé par l’équipe de Svante Wold et qui a permis de faire connaître cette méthode. Il est très complet et très orienté chimiométrie.
- XLSTAT : Avec des sorties très riches, XLSTAT vous permet de faire des régressions PLS directement dans Excel.
- JMP : Le logiciel user-friendly de SAS propose un outil complet pour les modèles de régression PLS.

Envie de maîtriser la régression PLS ?
Venez participer à notre prochaine formation à la régression PLS
Les évolutions de la régression PLS
La régression PLS a connu depuis quelques années de nombreuses évolutions méthodologiques en voici un petit florilège :
- La PLS discriminante qui consiste en une combinaison de régression PLS et d’analyse discriminante.
- La PLS non linéaire : la recherche de relations linéaires n’est pas nouvelle en PLS notamment avec des transformations préalables basées par exemple sur des splines mais aussi l’utilisation de combinaisons non linéaires pour construire les composantes PLS
- La sparse PLS pour les données parcimonieuses (avec le package spls de R)
- La régression logistique PLS basée sur le modèle logistique et la régression PLS
- La régression PLS généralisée
- …
Les possibilités avec la régression PLS sont très variées. N’hésitez pas à commenter cet article et à donner quelques exemples de développements et d’applications.
Partager cet article
